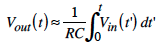Diode: one-way traffic

A diode is an electrical component which  has zero or very low resistance in one direction and infinite or very high resistance in the other. This characteristic allows electric current to flow in one direction only, the forward bias direction, while blocking current in the opposite, the reverse bias, direction.



I tested this property of the diode experimentally by measuring the resistance of a 1N914 diode in either direction. In one direction the resistance was too high (> 10 MΩ) and the multi-meter was overload. In the other direction, the resistance was ~ 0.5 MΩ (it was varying a lot with touching, since the resistance of the diode is temperature dependent :).

However, the 1N914 diode is not ideal (i.e. it does not have 0 and infinite resistance in the two electrodes). The curve shows the I-V relationship of a typical silicon diode.
This shows that a minimum of ~ 0.6V has to be applied across a forward-biased diode to make current flow through it. It also shows that the voltage drop remains almost constant at ~ 0.6 - 1 V.
The I-V curve also shows that V/I or R, is close to 0 at V > 0.6V, and very high for negative voltage, which is characteristic of the diode.



Half Wave Rectifier 

A rectifier is an electronic device which converts alternating current (AC), which is periodically switching direction of flow, to direct current (DC), which flows in one direction only.

During each positive half-cycle  of the AC sine wave, the diode is forward biased and current flows through. During each negative half of cycle, the diode is reverse biased and no current flows through it. This results in a Vout across the load R equal to Vs - VDiode for the positive half of the cycle, and 0 on the negative half.

HH Lab 3-2

I constructed the above half-wave rectifier circuit with a 2.2 kΩ resistor. The output was as expected, a half-wave rectified 60 Hz sine-wave. When the diode was connected in the forward-biased direction, the negative part of the 60 Hz AC could not get through, while when it was connected in the reverse-biase direction, the positive part was omitted as shown.

I wasn't being clever at all when taking these pictures, so I'll mention a few subtle details which are not obvious from these snapshots.

A smarter photographing would have shown this:








Vout = Vs - VDiode = 1.3 V - 0.6 V = 0.7 V
Period of 60 Hz AC ~ 16.7 msec
So, the period of half-wave is ~ 8.3 ms. However, the width of the rectified positive part of wave is shorter because no current flows when Vs < 0.6 V.

The second step towards AC-DC conversion is to smooth out the ripples. This can be done by adding a capacitor parallel to the resistor, which increases the "RC" time lag. If R is large enough so that RC >> 1/120 sec, then the capacitor will not discharge very much before it starts charging again, and the ripple will be small.

Here, I connected a 47 μF capacitor parallel to the 2.2 kΩ resistor, with Vs of 1.3 V.
Ripple amplitude is given by:

ΔV = 0.7V (1/60 x 2.2kΩ x 47μF) ~ 0.1 V.
This is what is seen in the scope :)

Signal Diodes HH Lab 3-5

I built the following circuit, which is a rectified differentiator, and drove it with a 10 kHz square wave.
The results obtained made sense, since it was a reminder of the square wave differentiated in last lab. However, this time the spikes did not appear in both direction, but only in the positive direction. This is expected since this is a rectified square wave!

Now, on zooming in closer, it can be seen that these "spikes" are RC discharge curves.

The signal on the scope is decaying with time constant, ~350ns.
R = t/C = 350ns/560pF ~ 600 Ω

If 1k and 2.2k are in parallel, effective R

R = 2.2/3.2 ~690 Ω

So I guess the two resistors are in parallel.
When I take the 2.2k out, the new time constant (I'm not too confident on this since I ddn't take a proper measurement) ~ 500ns
This corresponds to an R of ~ 0.9 k
On taking the 2.2k out, the 1 Meg of the scope kicks in. 
R = 1000/1001~ 1k

Makes somewhat sense, though I'm not entirely confident on the calculation.

Diode Limiter HH Lab 3-7

The diode can also be used to limit input voltages to < 0.6 V, which is useful for certain instruments which are sensitive to high voltages. The following circuit is called a diode limiter. If we remember the I-V curve at the top of the page, after crossing 0.6V barrier, the voltage drop across the diode becomes relatively constant - diode limiter takes advantage of this property. On driving it with sine, triangle and square wave, the following results were obtained:

As we can see, in all of the above cases, the Vout stays put at 0.6 V after we have crossed the point. It is also interesting to note how the triangle and sine wave changes their shape as Vin is increased. The edges of the wave rounds off, and they move towards becoming square waves. This is because signal over 0.6V is getting cut-off.

Impedances of Test Instruments

Ideal voltage measuring devices should have very high input impedance so as not to perturb the circuit. The input impedance of a scope comes from a 1MΩ  resistor in parallel with a 30 pF capacitor. The 30 pF is called stray capacitance since it is not put there intentionally. For a DC signal, this arrangement is fine since the capacitor provides infinite impedance. However, for high frequency signals the situation gets hairy as ZC gets smaller. We want ZC >> ZSignal under all circumstances, and hence special care has to be taken when dealing with high frequency sources.

To test the internal resistance of the scope, I connected a 1MΩ in series with the scope, driving it with a 10Vpp signal at 100 Hz. The output became halved as expected, showing that the internal resistance is also 1 MΩ.

On raising the frequency to a few kHz, the voltage drop increases further, and phase shift can be seen, show the effects of the stray capacitance. At 5 kHz, the Vpp is 2.8 V. Using this information, the capacitance of the circuit can be measured.

(Vin/Vout)^2 = 1+(ωRC)^2

(10.2/2.8)^2 - 1 = (5kHz x 1k x C)^-2

C ~ 10^-10 F ~ 100 pF

This is a bit bigger than I anticipated, maybe the capacitance from the cable adds up.
Also, I think I need to put in a factor of 2pi with the frequency, which will make it even bigger, almost a nF :(

A capacitor needs to be added in parallel to make this circuit work as a divide-by-two signal attenuator at all frequencies???

Capacitor - Storing it all

A capacitor is an electrical component used to store energy in an electric field. It consists of two electrical conductors separated by a dielectric. When there is a potential difference across the conductors of the capacitor, a static electric field develops across the dielectric, causing positive charge to collect on one of the plates and negative charge on the other. The energy is stored in the electrostatic field.

A voltage applied across a capacitor results in a build-up of charge in the two plates, and when the voltage source is removed, the capacitor discharges through a load (e.g. a resistor). The time taken for the charging and discharging depends on the value of R and C.

VR = IR
Vin(t)-Vout(t) = I(t)R
q(t) = CVout(t)
Vout(t) = q(t)/C
dVout(t)/dt = I(t)/C
I(t) ~ Vin(t)/R
dVout(t)/dt ~ 1/RC Vin(t)

Time constant = RC
The capacitor introduces a time lag, RC, in the response of the circuit.

Voltage across a charging capacitor:

Voltage across a discharging capacitor:




HH Lab 2-1

This little experiment explores the behavior of an RC circuit in the time-domain. We are looking at the Vout across a 0.01μF capacitor connected to a 10 kΩ resistor. We are driving the circuit with square waves through a function generator. 

Here we have applied a 500Hz square-wave. The time constant of the circuit is:

RC = 10 kΩ x 0.01μF = 0.1 ms

The period of the square wave is 2 ms, much bigger than the time constant, hence we can observe the charging and discharging in action on the two sides of the wave but the squareness is preserved.

In this one, the frequency of square wave is 1 kHz, hence the period is 1ms, closer to the time-constant, and we can see the squareness of the wave getting more distorted as the charging and discharging can be seen more clearly.

Here the frequency is 10kHz, with period 0.1 ms, smaller than the time constant. Hence the square is distorted completely and only the charging and discharging can be seen.

Using the 1 kHz figure to do the calculation, 

Time to climb from 0% to 63% ~ 26 μs ~ 0.2 ms ~ RC

Time to fall to 37% ~ 24 μs ~ 0.2 ms ~ RC

LogoChip Capacitance Meter

Using the LogoChip we built a simple capacitance meter. The program measures the time it takes for the charge in the capacitor to build to some particular value. Since this time depends on the RC time, and R is constant, by measuring time we can deduce C.
I first measured the time for a singe 0.1μF. The value I was expecting is:
t=RC=100kΩx0.1μF = 0.01s = 10 ms
The number I found is 11 (in ms). Close enough!

Next two 0.1μF in parallel. Parallel capacitance adds up, so the total capacitance is 0.2μF. I'm expecting the number 20, and we got it!
For two 0.1μF in series the total capacitance is 0.05μF, and hence the time should be 5. Bingo!!

Integrator (HH Lab 2-3)

For an RC circuit:
That is the output function is an integral of the input function.
From the experiment above we saw that as we reduced the period of the Vin, so that it was within the range of the time constant of the circuit, the square wave changed its shape to triangle wave - which is what we get by integrating a square wave. Hence the above circuit can be used as an integrator of functions, as long as the time constant of the RC circuit is bigger than the period of the input function. Or in other words, the input of the frequency signal has to sufficiently high so that:

In this circuit, 1/RC = 10 kHz. So, I drove it with 100 kHz square (pictured), sine and triangle wave. The blue signal is the input and yellow is the output. As expected, I found a triangle wave as the integral of a square wave. For a triangle wave function, the integral was a sine wave and for a sine wave the integral was another sine wave, 180 out of phase.
Notice that the amplitude of Vout is much smaller than that of Vin.

Differentiator (HH Lab 2-2)

If this circuit is smart enough to integrate then one can hope that it should be able to differentiate as well! And it can, at sufficiently low frequency.

Notice that unlike the integrator, here we are looking at the output across the resistor and not the capacitor.
Here, 1/RC = 100 MHz
For differentiator, the following must be satisfied:

We drove the circuit with square, triangle and sine wave at 100kHz. All the outputs were as expected the derivative of the respective functions. The square wave which consists of a number of high frequency spikes followed by flat lines (0 frequency), has the derivative which shows just that. Each of these spikes, on closer look, turned out to be RC discharge curves (to be discussed later). The triangle wave is positive and negative slopes alternating sharply, so gave a square wave output. The derivative of a sine wave is a sine wave, 180 out of phase.
I also tried sine wave at 0 (1mHz) and infinite (10 MHz) frequency. As expected, the impedance of the capacitor at 0 (DC) frequency is infinite, so the Vout across the resistor was equal to Vin. At infinite frequency, the impedance of the capacitor is 0, so the Vout across the resistor was 0.

Next, we increased the RC by a factor of a thousand of 1000. The new 1/RC = 100 kHz. When we drive the circuit at 100 kHz as well, it doesn't satisfy the condition of ω >> 1/RC, and the differentiator fails as can be seen in the picture. Interesting point to note here is that the input signal is distorted as well. 


Low Pass Filter (HH Lab 2-4)

Electronic filters takes advantage of the frequency dependence of complex impedance of the capacitor to attenuate low/high frequencies.
For low-pass filter, Vout << Vin for high frequency signals and hence they are attenuated. This circuit is similar to integrator circuit.

-3db frequency is the frequency at which the signal attenuates to 1/√2 or 0.707 Vmax. 
f-3DB = 1/2πRC = 1.1 kHz (calculated)
We first used the sweep function of the signal generator (video), and later manually changed the frequency of input to find:
f-3DB ~ 1 kHz (measured), matches!!!

At very low frequencies, when the impedance of the circuit is nearly equal to the resistance, the limiting phase shift is 0 (in phase). At high frequencies the limiting phase shift is 90°, because the reactance of the capacitor is large compared to the resistor. 

Phase shifts:





f << f-3DB ---> no phase shift (1/1+i(0)RC = 1; same phase)
f = f-3DB ---> 45° (1/√2; π/2)
f >> f-3DB ---> 90° (1/-i; π)

High Pass Filter (HH Lab 2-5)

For high-pass filter, Vout << Vin for low frequency signals and hence they are attenuated. This circuit is similar to the differentiator circuit.
f-3DB = 1/2πRC = 1.1 kHz (calculated) same as low-pass
f-3DB ~ 1 kHz (measured), again matches!

The limiting phase shifts are opposite to that of the low-pass filter. At very low frequencies, the limiting phase shift is 90°, while at high frequencies the limiting phase shift is 0. 


Garbage Detector (HH Lab 2-6)

The 110V ac voltage we get from our mains supply is at 60 Hz, but has a lot of craps at other frequencies, especially at higher frequency. These crap can be see through a high-pass filter, because it attenuates the 60 Hz main, and lets through the higher frequency signals. For this circuit,

f3DB = 1/(2πRC) = 1/(2π x 15k x 0.01μF) = 1 kHz

Number of octaves for 1kHz to be 60Hz (1000-500-250-125-62.5) = 4 octaves

Attenuation = 1/2^4 = 1/16

From the scope,

Vin = 6.4V

Vout = 0.38 V

Vout/Vin = 0.38/6.4 = 1/16  .... just as I expected!!! 

Blocking Capacitor (HH Lab 2-8)

Blocking capacitor is useful for putting an offset on an ac signal. The blocking capacitor prevents the dc voltages to pass through, allowing only ac signals. Hence, the ac voltage will "ride on top of" the 5 V (15Vx 5k/15k) dc voltage supplied by the voltage divider.

Now, why the pain of going through blocking capacitor? Why not hook the two power sources up directly? Its because power supply with smaller output impedance wins the tug of war between multiple power sources hooked up together. The output resistance of the voltage divider is ~ 680Ω, while that of the function generator is 50Ω. Hence, if the capacitor is not present, the function generator will win the tug-of-war and only its output can be seen on the scope. By inserting a very small capacitor in series with the function generator, we increased the impedance of this branch of the circuit. This branch now becomes a high pass filter with all signals of interest above the 3 dB point. Using the circuit A above, we did get an offset of 5V.
Low frequency limit,
f-3DB = 1/2πRC =  1/2πx3.2kΩx4.7μF = 10Hz