A capacitor is an electrical component used to store energy in an electric field. It consists of two electrical conductors separated by a dielectric. When there is a potential difference across the conductors of the capacitor, a static electric field develops across the dielectric, causing positive charge to collect on one of the plates and negative charge on the other. The energy is stored in the electrostatic field.
 A voltage applied across a capacitor results in a build-up of charge in the two plates, and when the voltage source is removed, the capacitor discharges through a load (e.g. a resistor). The time taken for the charging and discharging depends on the value of R and C.
A voltage applied across a capacitor results in a build-up of charge in the two plates, and when the voltage source is removed, the capacitor discharges through a load (e.g. a resistor). The time taken for the charging and discharging depends on the value of R and C.VR = IR
Vin(t)-Vout(t) = I(t)R
q(t) = CVout(t)
Vout(t) = q(t)/C
dVout(t)/dt = I(t)/C
I(t) ~ Vin(t)/R
dVout(t)/dt ~ 1/RC Vin(t)
Time constant = RC
The capacitor introduces a time lag, RC, in the response of the circuit.

Voltage across a charging capacitor:

Voltage across a discharging capacitor:

HH Lab 2-1
This little experiment explores the behavior of an RC circuit in the time-domain. We are looking at the Vout across a 0.01μF capacitor connected to a 10 kΩ resistor. We are driving the circuit with square waves through a function generator.
Here we have applied a 500Hz square-wave. The time constant of the circuit is:
RC = 10 kΩ x 0.01μF = 0.1 ms
The period of the square wave is 2 ms, much bigger than the time constant, hence we can observe the charging and discharging in action on the two sides of the wave but the squareness is preserved.

In this one, the frequency of square wave is 1 kHz, hence the period is 1ms, closer to the time-constant, and we can see the squareness of the wave getting more distorted as the charging and discharging can be seen more clearly.
Here the frequency is 10kHz, with period 0.1 ms, smaller than the time constant. Hence the square is distorted completely and only the charging and discharging can be seen.
Using the 1 kHz figure to do the calculation,
Time to climb from 0% to 63% ~ 26 μs ~ 0.2 ms ~ RC
Time to fall to 37% ~ 24 μs ~ 0.2 ms ~ RC
LogoChip Capacitance Meter
 Using the LogoChip we built a simple capacitance meter. The program measures the time it takes for the charge in the capacitor to build to some particular value. Since this time depends on the RC time, and R is constant, by measuring time we can deduce C.
Using the LogoChip we built a simple capacitance meter. The program measures the time it takes for the charge in the capacitor to build to some particular value. Since this time depends on the RC time, and R is constant, by measuring time we can deduce C.
I first measured the time for a singe 0.1μF. The value I was expecting is:
t=RC=100kΩx0.1μF = 0.01s = 10 ms
The number I found is 11 (in ms). Close enough!
Next two 0.1μF in parallel. Parallel capacitance adds up, so the total capacitance is 0.2μF. I'm expecting the number 20, and we got it!
For two 0.1μF in series the total capacitance is 0.05μF, and hence the time should be 5. Bingo!!
Integrator (HH Lab 2-3)
 Using the LogoChip we built a simple capacitance meter. The program measures the time it takes for the charge in the capacitor to build to some particular value. Since this time depends on the RC time, and R is constant, by measuring time we can deduce C.
Using the LogoChip we built a simple capacitance meter. The program measures the time it takes for the charge in the capacitor to build to some particular value. Since this time depends on the RC time, and R is constant, by measuring time we can deduce C.I first measured the time for a singe 0.1μF. The value I was expecting is:
t=RC=100kΩx0.1μF = 0.01s = 10 ms
The number I found is 11 (in ms). Close enough!
Next two 0.1μF in parallel. Parallel capacitance adds up, so the total capacitance is 0.2μF. I'm expecting the number 20, and we got it!
For two 0.1μF in series the total capacitance is 0.05μF, and hence the time should be 5. Bingo!!
Integrator (HH Lab 2-3)

For an RC circuit:
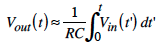
That is the output function is an integral of the input function.
From the experiment above we saw that as we reduced the period of the Vin, so that it was within the range of the time constant of the circuit, the square wave changed its shape to triangle wave - which is what we get by integrating a square wave. Hence the above circuit can be used as an integrator of functions, as long as the time constant of the RC circuit is bigger than the period of the input function. Or in other words, the input of the frequency signal has to sufficiently high so that:

In this circuit, 1/RC = 10 kHz. So, I drove it with 100 kHz square (pictured), sine and triangle wave. The blue signal is the input and yellow is the output. As expected, I found a triangle wave as the integral of a square wave. For a triangle wave function, the integral was a sine wave and for a sine wave the integral was another sine wave, 180 out of phase.
Notice that the amplitude of Vout is much smaller than that of Vin.

Notice that the amplitude of Vout is much smaller than that of Vin.

Differentiator (HH Lab 2-2)
 If this circuit is smart enough to integrate then one can hope that it should be able to differentiate as well! And it can, at sufficiently low frequency.
If this circuit is smart enough to integrate then one can hope that it should be able to differentiate as well! And it can, at sufficiently low frequency.
 Notice that unlike the integrator, here we are looking at the output across the resistor and not the capacitor.
Notice that unlike the integrator, here we are looking at the output across the resistor and not the capacitor.Here, 1/RC = 100 MHz
For differentiator, the following must be satisfied:

 We drove the circuit with square, triangle and sine wave at 100kHz. All the outputs were as expected the derivative of the respective functions. The square wave which consists of a number of high frequency spikes followed by flat lines (0 frequency), has the derivative which shows just that. Each of these spikes, on closer look, turned out to be RC discharge curves (to be discussed later). The triangle wave is positive and negative slopes alternating sharply, so gave a square wave output. The derivative of a sine wave is a sine wave, 180 out of phase.
We drove the circuit with square, triangle and sine wave at 100kHz. All the outputs were as expected the derivative of the respective functions. The square wave which consists of a number of high frequency spikes followed by flat lines (0 frequency), has the derivative which shows just that. Each of these spikes, on closer look, turned out to be RC discharge curves (to be discussed later). The triangle wave is positive and negative slopes alternating sharply, so gave a square wave output. The derivative of a sine wave is a sine wave, 180 out of phase.I also tried sine wave at 0 (1mHz) and infinite (10 MHz) frequency. As expected, the impedance of the capacitor at 0 (DC) frequency is infinite, so the Vout across the resistor was equal to Vin. At infinite frequency, the impedance of the capacitor is 0, so the Vout across the resistor was 0.

Next, we increased the RC by a factor of a thousand of 1000. The new 1/RC = 100 kHz. When we drive the circuit at 100 kHz as well, it doesn't satisfy the condition of ω >> 1/RC, and the differentiator fails as can be seen in the picture. Interesting point to note here is that the input signal is distorted as well.
Low Pass Filter (HH Lab 2-4)
For low-pass filter, Vout << Vin for high frequency signals and hence they are attenuated. This circuit is similar to integrator circuit.
-3db frequency is the frequency at which the signal attenuates to 1/√2 or 0.707 Vmax.
f-3DB = 1/2πRC = 1.1 kHz (calculated)
We first used the sweep function of the signal generator (video), and later manually changed the frequency of input to find:
f-3DB ~ 1 kHz (measured), matches!!!
At very low frequencies, when the impedance of the circuit is nearly equal to the resistance, the limiting phase shift is 0 (in phase). At high frequencies the limiting phase shift is 90°, because the reactance of the capacitor is large compared to the resistor.

Phase shifts:

f << f-3DB ---> no phase shift (1/1+i(0)RC = 1; same phase)
f = f-3DB ---> 45° (1/√2; π/2)
f >> f-3DB ---> 90° (1/-i; π)
High Pass Filter (HH Lab 2-5)
For high-pass filter, Vout << Vin for low frequency signals and hence they are attenuated. This circuit is similar to the differentiator circuit.
f-3DB = 1/2πRC = 1.1 kHz (calculated) same as low-pass
f-3DB ~ 1 kHz (measured), again matches!
The limiting phase shifts are opposite to that of the low-pass filter. At very low frequencies, the limiting phase shift is 90°, while at high frequencies the limiting phase shift is 0.
Garbage Detector (HH Lab 2-6)
 The 110V ac voltage we get from our mains supply is at 60 Hz, but has a lot of craps at other frequencies, especially at higher frequency. These crap can be see through a high-pass filter, because it attenuates the 60 Hz main, and lets through the higher frequency signals. For this circuit,
The 110V ac voltage we get from our mains supply is at 60 Hz, but has a lot of craps at other frequencies, especially at higher frequency. These crap can be see through a high-pass filter, because it attenuates the 60 Hz main, and lets through the higher frequency signals. For this circuit,
Blocking Capacitor (HH Lab 2-8)
Blocking capacitor is useful for putting an offset on an ac signal. The blocking capacitor prevents the dc voltages to pass through, allowing only ac signals. Hence, the ac voltage will "ride on top of" the 5 V (15Vx 5k/15k) dc voltage supplied by the voltage divider.
Now, why the pain of going through blocking capacitor? Why not hook the two power sources up directly? Its because power supply with smaller output impedance wins the tug of war between multiple power sources hooked up together. The output resistance of the voltage divider is ~ 680Ω, while that of the function generator is 50Ω. Hence, if the capacitor is not present, the function generator will win the tug-of-war and only its output can be seen on the scope. By inserting a very small capacitor in series with the function generator, we increased the impedance of this branch of the circuit. This branch now becomes a high pass filter with all signals of interest above the 3 dB point. Using the circuit A above, we did get an offset of 5V.
Low frequency limit,
f-3DB = 1/2πRC = 1/2πx3.2kΩx4.7μF = 10Hz
For high-pass filter, Vout << Vin for low frequency signals and hence they are attenuated. This circuit is similar to the differentiator circuit.
f-3DB = 1/2πRC = 1.1 kHz (calculated) same as low-pass
f-3DB ~ 1 kHz (measured), again matches!
The limiting phase shifts are opposite to that of the low-pass filter. At very low frequencies, the limiting phase shift is 90°, while at high frequencies the limiting phase shift is 0.
Garbage Detector (HH Lab 2-6)
 The 110V ac voltage we get from our mains supply is at 60 Hz, but has a lot of craps at other frequencies, especially at higher frequency. These crap can be see through a high-pass filter, because it attenuates the 60 Hz main, and lets through the higher frequency signals. For this circuit,
The 110V ac voltage we get from our mains supply is at 60 Hz, but has a lot of craps at other frequencies, especially at higher frequency. These crap can be see through a high-pass filter, because it attenuates the 60 Hz main, and lets through the higher frequency signals. For this circuit,
f3DB = 1/(2πRC) = 1/(2π x 15k x 0.01μF) = 1 kHz
Number of octaves for 1kHz to be 60Hz (1000-500-250-125-62.5) = 4 octaves
Attenuation = 1/2^4 = 1/16
From the scope,
Vin = 6.4V
Vout = 0.38 V
Vout/Vin = 0.38/6.4 = 1/16 .... just as I expected!!!
Blocking capacitor is useful for putting an offset on an ac signal. The blocking capacitor prevents the dc voltages to pass through, allowing only ac signals. Hence, the ac voltage will "ride on top of" the 5 V (15Vx 5k/15k) dc voltage supplied by the voltage divider.
Now, why the pain of going through blocking capacitor? Why not hook the two power sources up directly? Its because power supply with smaller output impedance wins the tug of war between multiple power sources hooked up together. The output resistance of the voltage divider is ~ 680Ω, while that of the function generator is 50Ω. Hence, if the capacitor is not present, the function generator will win the tug-of-war and only its output can be seen on the scope. By inserting a very small capacitor in series with the function generator, we increased the impedance of this branch of the circuit. This branch now becomes a high pass filter with all signals of interest above the 3 dB point. Using the circuit A above, we did get an offset of 5V.
Low frequency limit,
f-3DB = 1/2πRC = 1/2πx3.2kΩx4.7μF = 10Hz








No comments:
Post a Comment